小学四年级图形面积题

本来今天高高兴兴，你为什么要叫我学图形面积？

蓝 瘦  香 菇

相信很多家长都听过孩子的抱怨：“图形面积好难啊，压根儿不会！”、“这次考试又没考好，图形面积题分都拿不了。”是图形面积真的难吗？不！教你三招，包你搞定图形面积！

第一招：逢山开路。

解题过程中难免遇上阻碍前进的大山，而我们所要做的就是开辟道路，穿山而过。很多图形面积难题实际上都是由我们所学过的基本图形组合而来，因此，记住基础图形的面积公式是孩子解题必备的工具。工欲善其事，必先利其器。只有牢牢掌握基础公式，遇见难题时，才能步步分解，把难题的“难”化作基础知识能解决的“易”，各个击破，攻克难题。

第二招：遇水搭桥。

解题道路上可乏险山恶水，遇山要开路，逢水便搭桥。

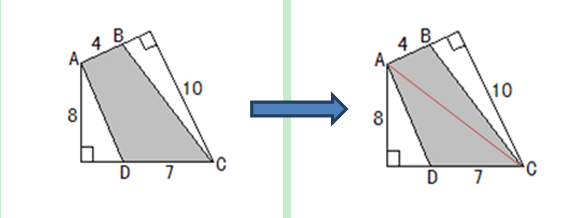
“辅助线”便是我们遇见恶水所需要搭的桥。很多图形面积题目并没有直观的思路去解题，很多人看见汹涌的河水便畏惧了，而不敢常识着去搭桥。结合辅助线，我们常用的方法便是：

（一）大面积减小面积。

（二）割补法。

（三）中介法。

（四）面积转移法。

以上方法，结合辅助线搭的桥，许多难题便可迎“线”而解。

第三招：乾坤大挪移。

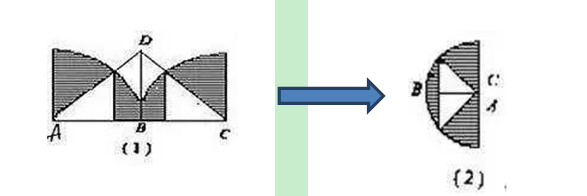
图形面积除了从部分入手，进行切割转移以外，还可以从整体入手，改天换地，挪动位置，使得原本复杂的不规则的图形变得自然和谐。通常，涉及到圆的图形就可以考虑一下是否可以旋转使得题目变得简单，因为我们知道圆其实是一个十分特殊的图形，拥有无数条对称轴，利用圆的这个性质，遇见难题多做图形旋转，即可化解难题。

学会以上三招，数学中的图形面积题目的分数皆可收入囊中。不知看见妙招的你，是否已经开始行动了呢？