排列组合例题讲解

前面我们已讨论了加法原理、乘法原理、排列、组合等问题.事实上，这些问题是相互联系、不可分割的.例如有时候，做某件事情有几类方法，而每一类方法又要分几个步骤完成，如排列组合.在计算做这件事的方法时，既要用到乘法原理，又要用到加法原理.又如，在照相时，如果对坐的位置有些规定，那么就不再是简单的排列问题了.类似的问题有很多，要正确地解决这些问题，就一定要熟练地掌握两个原理和排列、组合的内容，并熟悉它们所解决问题的类型特点.

看下面排列组合例题.

例1 由数字0、1、2、3可以组成多少个没有重复数字的偶数？

分析 注意到由四个数字0、1、2、3可组成的偶数有一位数、二位数、三位数、四位数这四类，所以要一类一类地考虑，再由加法原理解决.

第一类：一位偶数只有0、2，共2个；

第二类：两位偶数，它包含个位为0、2的两类.若个位取0，则十位可有C13种取法；若个位取2，则十位有C12种取法.故两位偶数共有（C13＋C12）种不同的取法；

第三类：三位偶数，它包含个位为0、2的两类.若个位取0，则十位和百位共有P23种取法；若个位取2，则十位和百位只能在0、1、3中取，百位有2种取法，十位也有2种取法，由乘法原理，个位为2的三位偶数有2×2个，三位偶数共有（P23＋2×2）个；

第四类：四位偶数.它包含个位为0、2的两类.若个位取 0，则共有P33个；若个位取 2，则其他 3位只能在 0、 1、 3中取.千位有2种取法，百位和十位在剩下的两个数中取，再排成一列，有P22种取法.由乘法原理，个位为2的四位偶数有2×P22个.所以，四位偶数共有（P33＋2×P22）种不同的取法.

解： 由加法原理知，共可以组成

2＋（C13＋C12）＋（P23＋2×2）＋（P33＋2×P22）

＝2＋5＋10＋10

＝27

个不同的偶数.

补充说明：本题也可以将所有偶数分为两类，即个位为0和个位为2的两类.再考虑到每一类中分别有一位、两位、三位、四位数，逐类讨论便可求解.

例2 国家举行足球赛，共15个队参加.比赛时，先分成两个组，第一组8个队，第二组7个队.各组都进行单循环赛（即每个队要同本组的其他各队比赛一场）.然后再由各组的前两名共4个队进行单循环赛，决出冠亚军.问：①共需比赛多少场？②如果实行主客场制（即A、B两个队比赛时，既要在A队所在的城市比赛一场，也要在B队所在的城市比赛一场），共需比赛多少场？

分析 比赛的所有场次包括三类：第一组中比赛的场次，第二组中比赛的场次，决赛时比赛的场次.

①中，第一组中8个队，每两队比赛一场，所以共比赛C28场；第二组中7个队，每两队比赛一场，所以共比赛C27场；决赛中4个队，每两队比赛一场，所以共比赛C24场.②中，由于是实行主客场制，每两个队之间要比赛两场，比赛场次是①中的2倍.

另外，还可以用排列的知识来解决.由于主客场制不仅与参赛的队有关，而且与比赛所在的城市（即与顺序）有关.所以，第一组共比赛P28场，第二组共比赛P27场，决赛时共比赛P24场.

解： 由加法原理：

①实行单循环赛共比赛

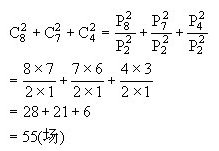
②实行主客场制，共需比赛

2×（C28＋C27＋C24）＝110（场）.

或解为：

P28＋P27＋P24

＝8×7＋7×6＋4×3

＝56＋42＋12

＝110（场）.

例3 在一个半圆周上共有12个点，如下图，以这些点为顶点，可以画出多少个 ①三角形？②四边形？

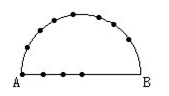
分析 ①我们知道，不在同一直线上的三个点确定一个三角形，由图可见，半圆弧上的每三个点均不共线（由于A、B既可看成半圆上的点，又可看成线段上的点，为不重复计算，可把它们归在线段上），所以，所有的三角形应有三类：第一类，三角形的三个顶点全在半圆弧上取（不含A、B两点）；第二类，三角形的两个顶点取在半圆弧上（不包含A、B），另一个顶点在线段上取（含A、B）；第三类，三角形的一个顶点在半圆弧上取，另外两点在线段上取.

注意到三角形的个数只与三个顶点的取法有关，而与选取三点的顺序无关，所以，这是组合问题.

解：三个顶点都在半圆弧上的三角形共有

两个顶点在半圆弧上，一个顶点在线段上的三角形共有

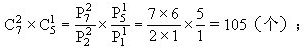
一个顶点在半圆弧上，两个顶点在线段上的三角形共有

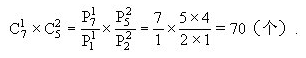
由加法原理，这12个点共可以组成

C37＋（C27×C15）＋（C17×C25）

＝35＋105＋70＝210（个）

不同的三角形.

也可列式为C312－C35＝220—10＝210（个）.

分析 ②用解①的方法考虑.

将组成四边形时取点的情况分为三类：

第一类：四个点全在圆弧上取.（不包括A、B）有C17种取法.

第二类：两个点取自圆弧.两个点取自直线AB.有取法C27×C25种.

第三类：圆弧上取3个点，直线上取1个点，有C37×C15种取法.

解： 依加法原理，这12个点共可组成：

C47+ C27×C25+C37×C15

＝35＋210＋175＝420

个不同的四边形.

还可直接计算，这12个点共可组成：

C412-C45-C35·C17＝495－5-70＝420个不同的四边形.

例4 如下图，问

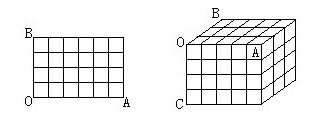
①下左图中，有多少个长方形（包括正方形）？

②下右图中，有多少个长方体（包括正方体）？

分析 ①由于长方形是由两组分别平行的线段构成的，因此只要看上左图中水平方向的所有平行线中，可以选出几组两条平行线，竖直方向上的所有平行线中，可以选出几组两条平行线？

②由于长方体是由三组分别平行的平面组成的.因此，只要看上页右图中，平行于长方体上面的所有平面中，可以选出几组两个互相平行的平面，平行于长方体右面的所有平面中，可以选出几组两个互相平行的两个平面，平行于长方体前面的所有平面中，可以选出几组两个互相平行的平面.

解： ①C25×C27＝210（个）

因此，上页左图中共有210个长方形.

②C25×C26×C24＝900（个）、

因此，上页右图中共有900个长方体.

例5 甲、乙、丙、丁4人各有一个作业本混放在一起，4人每人随便拿了一本，问：

①拿到自己作业本的拿法有多少种？

②恰有一人拿到自己作业本的拿法有多少种？

③至少有一人没有拿到自己作业本的拿法有多少种？

④谁也没有拿到自己作业本的拿法有多少种？

分析 ①甲拿到自己的作业本，这时只要考虑剩下的三个人拿到其他三本作业本的情况.由于其他三人可以拿到自己的作业本，也可以不拿到自己的作业本.所以，共有P33种情况.

②恰有一人拿到自己的作业本.这时，一人拿到了自己的作业本，而其他三人都没能拿到自己的作业本.拿到自己作业本的可以是甲、乙、丙、丁中的一人，共4种情况.另外三人全拿错了作业本的拿法有2种.故恰有一人拿到自己作业本的情况有4×2种情况.

③至少有一人没有拿到自己的作业本.这时只要在所有拿法中减去四人全拿到自己作业本的拿法即可.由于4人拿作业本的所有拿法是P44，而4人全拿到自己作业本只有1种情况.所以，至少有一人没拿到自己作业本的拿法有P44－1种情况.

④谁也没拿到自己的作业本.可分步考虑（假设四个人一个一个地拿作业本，考虑四人都拿错的情况即可）.第一个拿作业本的人除自己的作业本外有3种拿法.被他拿走作业本的人也有3种拿法.这时，剩下的两人只能从剩下的两本中拿，要每人都拿错，只有一种拿法.所以，由乘法原理，共有3×3×1种不同的情况.

解:①甲拿到自己作业本的拿法有P33＝3×2×1＝ 6种情况；

②恰有一人拿到自己作业本的拿法有4×2＝8种情况；

③至少有一人没有拿到自己作业本的拿法有P44－1＝4×3×2×1－1＝23种情况；

④谁也没有拿到自己作业本的拿法有3×3×1＝9种情况.

由前面的各例题可以看到，有关排列组合的问题多种多样，思考问题的方法灵活多变，入手的角度也是多方面的.所以，除掌握有关的原理和结论，还必须学习灵活多样的分析问题、解决问题的方法.