小学数学牛吃草问题

牛吃草问题又称为消长问题或牛顿牧场，是17世纪英国伟大的科科学家牛顿提出来的。典型牛吃草问题的条件是假设草的生长速度固定不变，不同数量的牛吃光同一片草地所需的天数各不相同，求若干头牛吃这片草地可以吃多少天。由于吃的天数不同，草又是天天在生长的，所以草的存量随牛吃的天数不断地变化。解决牛吃草问题常用到四个基本公式分别是：

(1)草的生长速度=(相应的牛的头数×吃的较多天数-相应的牛的头数×吃的较少天数)÷(吃的较多天数-吃的较少天数)；

(2)原有草量=牛的头数×吃的天数-草的生长速度×吃的天数；

(3)吃的天数=原有草量÷(牛的头数-草的生长速度)；

(4)牛的头数=原有草量÷吃的天数+草的生长速度。

这四个公式是解决消长问题的基础。

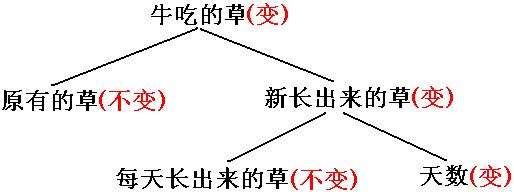
由于牛在吃草的过程中，草是不断生长的，所以解决消长问题的重点是要想办法从变化中找到不变量。牧场上原有的草是不变的，新长的草虽然在变化但由于是匀速生长，所以每天新长出的草量应该是不变的。正是由于这个不变量，才能够推导出上面的四个基本公式。

牛吃草问题经常给出不同头数的牛吃同一片地的草，这块地既有原有的草，又有每天新长出的草。由于吃草的牛的头数不同，求若干头牛吃的这片地的草可以吃多少天。

这类问题的基本数量关系是：

1.牛的头数×(吃草较多的天数-吃草较少的天数)÷(吃的较多的天数-吃的较少的天数)=草地每天新长草的量。

2.牛的头数×吃草天数-每天新长量×吃草天数=草地原有的草。

解题关键是弄清楚已知条件，进行对比分析，从而求出每日新长草的数量，再求出草地里原有草的数量，进而解答题总所求的问题。