小学数学知识点：探索规律

【图表梳理】

【知识要点】

1. 间隔（植树等）问题

当甲、乙两个物体间隔排列时，如果两端都是甲物体，那么甲物体就比乙物体多 1 个。间隔问题在生活中有着广泛的应用，比较典型的就是植树问题。在一定长度的路线上，等距离地安排植树点，那么植树棵数、株距及路线总长度有下面的关系：

（1）两端都植树：棵数 = 路长÷株距 +1

（2）两端都不植树：棵数 = 路长÷株距 -1

（3）只有一端植树或者是在封闭的路线上植树：棵数 = 路长÷株距

2. 搭配排列问题

搭配排列问题的常用解题方法：（1）连线计数（2）列举（3）根据乘法原理列式计算

3. 周期问题

周期问题：事物按一定的规律，周而复始地循环出现的一种现象。

周期问题解题的关键是找准周期，主要解题方法有：

（1）在图中画一画圈一圈（2）列举（3）根据规律列式计算 4. 简单覆盖问题

求覆盖次数的常用方法：

（1）用平移的方法来计数

（2）应用规律列式计算，计算公式是：

覆盖的总次数 = 横行覆盖次数 x 竖行覆盖次数

【学法指导】

1. 观察规律。要善于观察事物之间的相同点和不同点。

2. 发现规律。选择恰当的方法去发现规律，如：画图法、枚举法、列表法等。

3. 运用规律。理论与实践相结合，学以致用。

小学数学练习题：探索规律

例 1 一条马路长 440 米，在路的一旁每隔 8 米种一棵树，两端都种树，共种了多少棵树?

【分析】解答植树问题时，先要判断是在直线上植树，还是在封闭的路线上植树。这道题是在一条马路上也就是直线上植树，并且两端都植树。

【思路】路长 440 米，间隔长度 8 米，所以马路被分成 440÷8=55（段）。又因为两端都种树，所以植树棵数比间隔数多 1。

440÷8+1=56（棵）即共种了 56 棵树。

【回顾】题例中因为是两端植树，所以植树棵数比间隔数多 1。如果两端都不植，则植树棵数就应比间隔数少 1，可见求植树棵数时，要注意两端是否植树、间隔数与植树棵数之间的区别和联系。

例 2 小潘买来 3 件不同的上衣和 4 条不同的裤子，他一共可以有多少种不同的穿法?

【分析】这是一道典型的搭配问题，可以通过列举法进行列举，也可以画图，通过连线来解答。这两种方法都比较直观，便于从中发现这类问题的规律，从而理解用乘法计算的原理。

【思路】列举法和连线法请同学们自己完成。通过列举法和连线法可以发现，每一件上衣可以分别与 4 条裤子搭配着穿，有 4 种穿法；有 3 件上衣，一共有 3 个 4 种穿法，也就是有 12 种不同的穿法。

3x4=12（种）即他一共可以有 12 种不同的穿法。

【回顾】通过观察事物的特点，比较事物间的异同，从中发现可能具有的规律，这是探索事物规律的常用方法。我们需要学会和掌握这种探索规律的方法。

例 3 观察下表，表格里上、中、下一列为一组，第一组是（A，我，1），第二组是（B，爱，3）。

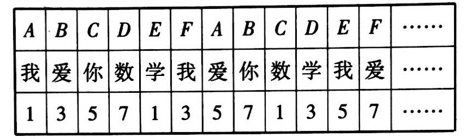
那么第 88 组是什么?

【分析】题例中把几个不同周期的问题综合在一道题里，这虽给解题增加了难度，但通过分析和解答，可加深我们对周期问题的理解，掌握不同周期问题的解答方法。

【思路】表格里上、中、下三行的排列都有各自的顺序和周期。第一行以“A，B，C，D，E，F"6 个字母为一周期，第二行以“我，爱，你，数，学”5 个文字为一周期，第三行以“1，3，5，7"4 个数为一周期，分别考虑三行的情况，找出第 88 组的排列。

第一行：88÷6=14.....4，余数是 4，所以第 -- 行第 88 个字母是 D；

第二行：88÷5=17.....3，余数是 3，所以第二行第 88 个文字是你；

第三行：88÷4=22，没有余数，所以第三行第 88 个数字是 7。

即第 88 组是（D，你，7）。

【回顾】解这道题时，我们采取的是先分后合的方法，先分成 3 行，分别找出规律，再将它们合起来。这种思考方法也是我们解答一些综合问题常用的方法。

例 4 在阳台一面墙上贴一块图案为

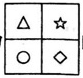
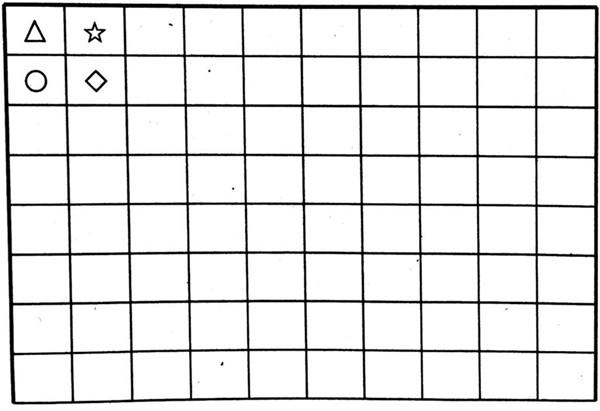
【分析】贴瓷砖是覆盖问题里最典型的实例，也是我们生活中常见的现象。本题例比较容易发现覆盖问题的规律，通过理解覆盖问题的解法，从而能更好地解答较为复杂的覆盖问题。

【思路】贴最上面一行有 10-2+1=9（种）贴法，贴最左边一列有 8-2+1=7（种）贴法。

10-2+1=9（种），8-2+1=7（种），9x7=63（种），即一共有 63 种不同的贴法。

【回顾】覆盖问题实际也是一种排列组合问题。从题例的解答中可以看出，要求有多少种贴法，就是先求出沿列和沿行分别有多少种贴法，然后用乘法求出一共有多少种贴法。掌握了这种方法，也为将来学习排列组合问题打牢了基础。