小学数学练习题：典型应用题

例1下表是张华同学单元练习的成绩记录情况，表中有两个数字不清楚，现用A、B来表示这两个数字。你知道张华同学的数学和英语的成绩各是多少分吗?

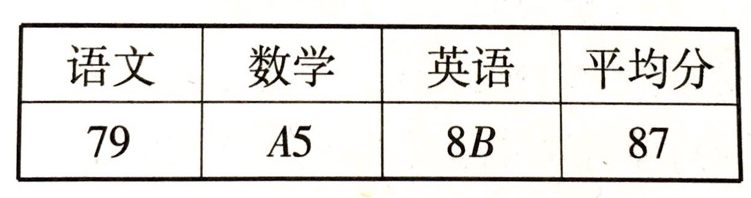
【分析】我们最常见的平均数实际问题是已知几个不相等的同类数量和份数，通过求出总数量后除以份数求出平均数。而在已知平均数的情况下，也可求出总数量后减去已知的部分量，求出未知的部分量。此题例就是这种实际应用问题。

【思路】要求数学英语各是多少分，先要根据三门学科的平均分求出三门学科的总分数，再减去语文成绩，就能得出数学和英语成绩的和。数学成绩的个位数字是5，就先从它们的和里减去5，而英语分数的十位数字是8，表示80，再减去80，那么得到的数就相当于是AB这个数，从而求出A和B分别代表多少，问题就迎刃而解了。

87x3-79=182（分），182-5-80=97（分）A是9，B是7，即数学和英语成绩分别是95分和87分。

【回顾】解决这道题时，我们先根据“平均数x份数=总数量”这个数量关系，求出三门学科的总分，然后运用逆向思维来推断两个字母分别代表的数字。学习平均数问题，既要会求出几个数量的平均数，又要能应用已知的平均数来解答相关的问题。

例2李师傅做一个机器零件由原来的12分钟减少到8分钟。原来做200个零件需要的时间，现在可以生产多少个?

【分析】这道题是归总问题，解答归总问题时，先要求出不变的总数量。这道题中，“总数量”是什么?是总时间还是零件总个数?分析题意可知，原来做零件的总个数与现在做零件的总个数肯定是变化的，所以本题例不变的量是总时间。

【思路】由原来做一个要12分钟，可以求出原来做200个零件共需要的时间。因为总时间一定，所以用总时间除以现在做一个零件需要的总时间，就得到现在能生产的零件个数。

（200x12）÷8=300（个），即现在可以生产300个零件。

例3甲、乙两人同时从两地骑自行车相向而行，甲每小时行15千米，乙每小时行13千米，两人在距中点3千米处相遇，求两地间的距离。

【分析】已知两人骑车的速度，要求两地的距离，根据相遇问题的思路，需要求出两人骑车的时间。这是解答本题的关键。

【思路】从题中可知甲骑得快，乙骑得慢，甲超过了中点3千米，乙距中点还少3千米，这就是说甲比乙多走的路程是3x2=6（千米），再根据路程差和速度差，就可求出相遇时间和两地距离。

（3x2）÷（15-13）x（15+13）=84（千米），即两地间的距离是84千米。

【回顾】解答这道题的难点是正确理解两人之间的路程差。题中“两人在距中点3千米处相遇”这一条件，不能理解为甲比乙多行3千米。

解答这道题时，我们是抓住“原来和现在所做的总时间是不变的”这一隐藏条件来解题的。归总问题的总量不变，归一问题的单一量不变，联系我们前面讲到的正、反比例的意义，试着发现其中的联系。

例4钢笔与圆珠笔每枝相差1元2角，小明带的钱买5枝钢笔差1元5角，买8枝圆珠笔多6角。问小明带了多少钱?

【分析】这道题属于较难的盈亏问题。我们先将它转化为同一对象一钢笔或者圆珠笔，然后再按盈亏问题的思路来解答。

【思路】小明带的钱买5枝钢笔差1元5角，我们可以将它转化成买5枝圆珠笔，因为每枝钢笔与每枝圆珠笔相差1元2角，这样把买5枝钢笔改成买5枝圆珠笔，就要省下6元钱，而原来还差1元5角，这时反而多出6元-1元5角=4元5角。这样我们就将原来的问题转化成了：小明带的钱买5枝圆珠笔多4元5角，买8枝圆珠笔多6角，问小明带了多少钱?这时我们就能很容易地求出这两种笔的价钱和小明带的钱数。

买5枝钢笔差1元5角，相当于买5枝圆珠笔多4元5角。每支圆珠笔的价钱是：（4。5-0。6）÷（8-5）=1。3（元），8x1。3+0。6=11（元），即小明带了11元。

【回顾】盈亏问题的解决方法其实是抓住两种方案的相差数，同时思考为什么会产生相差数，从而用相差的数量除以两次分得的差，就得到参加分配的数量。值得注意的是，在求两次分配方案的相差数时有三种不同情况：一次有余、一次不足，相差数=余+不足；两次都有余，相差数=大多余-小多余；两次都不足，相差数=大不足-小不足。

例5妈妈今年43岁，女儿今年11岁，几年后，妈妈的年龄是女儿的3倍?

【分析】这是一道年龄问题，题例告诉我们，如何抓住两人年龄差不变来解答这类问题。

【思路】女儿出生后，无论再过多少年，妈妈和女儿的年龄差总是不变的，即43-11=32（岁），这样就变成了一道已知两个人年龄差和两个人年龄之间倍数关系的差倍问题。把女儿几年后的岁数看做1倍数，妈妈的岁数看做3倍数，那么妈妈大的岁数就相当于女儿那时岁数的两倍，这样可以求出女儿那时的岁数。

43-11=32（岁），32÷（3-1）=16（岁），16-11=5（年）

即5年后，妈妈的年龄是女儿的3倍。

【回顾】解答有关年龄的问题时，要抓“年龄差不变”这--关键来分析思考，两人之间的年龄差是常量，不会随着时间的推移而改变。因为年龄问题常和和倍、差倍等问题综合在一起呈现，所以要注意根据问题的具体情境，选择恰当的方法来解答。