打破常规思维，从训练逻辑思维开始

打破常规思维，训练逆向思维能力，创新思维能力是现在的训练逻辑思维的重点。那么如何打破常规思维呢？还是要从训练逻辑思维能力开始。今天贤知助手就整理了一些逻辑思维能力题，一起来看看吧。

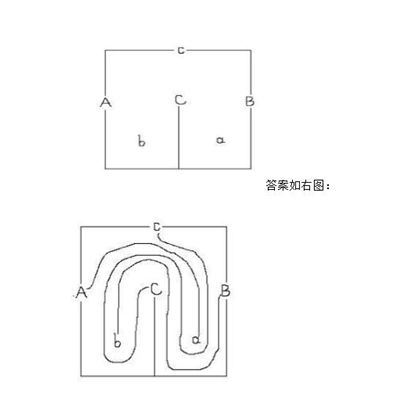
1、三个村庄A、B、C和三个城镇A、B、C坐落在如图所示的环形山内。由于历史原因，只有同名的村与镇之间才有来往。为方便交通，他们准备修铁路。问题是：如何在这个环形山内修三条铁路连通A村与A镇， B村与B镇，C村与C镇。而这些铁路相互不能相交。（挖山洞、修立交桥都不算，绝对是平面问题）。

2、2+7-2+7全部由火柴根组成，移动其中任何一根，答案要求为30说明：因为书写问题作如下解释，

2是由横折横三根组成，7是由横折两根组成1,改变赋值号.比如+,-,= 2,注意质数.

3,可能把画面颠倒过来.

4,然后就可以去考虑更改其他数字更改了

3、他们中谁的存活机率最大？

5个囚犯，分别按1-5号在装有100颗绿豆的麻袋抓绿豆，规定每人至少抓一颗，而抓得最多和最少的人将被处死，而且，他们之间不能交流，但在抓的时候，可以摸出剩下的豆子数。问他们中谁的存活几率最大？提示：

1，他们都是很聪明的人

2，他们的原则是先求保命，再去多杀人

3，100颗不必都分完

4，若有重复的情况，则也算最大或最小，一并处死

4、话说某天一艘海盗船被天下砸下来的一头牛给击中了,5个倒霉的家伙只好逃难到一个孤岛,发现岛上孤零零的,幸好有有棵椰子树,还有一只猴子!大家把椰子全部采摘下来放在一起,但是天已经很晚了,所以就睡觉先.

晚上某个家伙悄悄的起床,悄悄的将椰子分成5份,结果发现多一个椰子,顺手就给了幸运的猴子,然后又悄悄的藏了一份,然后把剩下的椰子混在一起放回原处,最后还是悄悄滴回去睡觉了.过了会儿,另一个家伙也悄悄的起床,悄悄的将剩下的椰子分成5份,结果发现多一个椰子,顺手就又给了幸运的猴子,然后又悄悄滴藏了一份,把剩下的椰子混在一起放回原处,最后还是悄悄滴回去睡觉了.总之5个家伙都起床过,都做了一样的事情。早上大家都起床,各自心怀鬼胎的分椰子了,这个猴子还真不是一般的幸运,因为这次把椰子分成5分后居然还是多一个椰子,只好又给它了.问题来了,这堆椰子最少有多少个?

5、10箱黄金，每箱100块，每块一两。有贪官，把某一箱的每块都磨去一钱。请称一次找到不足量的那个箱子

6、有十瓶药，每瓶里都装有100片药，其中有八瓶里的药每片重10克，另有两瓶里的药每片重9克。用一个蛮精确的小秤，只称一次，如何找出份量较轻的那两个药瓶？

答案：

1、

2、把第二个加号移去一根火柴2+7变成217

第一个加号加一根火柴.2+7变成247

247-217=30

3、由题设条件可知：摸到最大绿豆数的囚犯必死,摸到最小绿豆数的囚犯必死,摸到重复绿豆数的囚犯必死.

整体来看,至少有两个囚犯必死.绿豆数为5时,2个囚犯必死(11111).绿豆数为4时,3-4个囚犯必死(1211,2111).绿豆数为3时,4-5个囚犯必死(131,311,221,212).绿豆数为2、1时,5个囚犯必死.

5个囚犯的策略应该是：5个囚犯必须使摸到的绿豆数不重复,这样才会有最多存活机会；又必须使自己摸到的绿豆数居中,才会有最大存活机会.

明确了这一点,就可以往下分析了.

具体分析求机率

设1号囚犯摸到的绿豆数为N.

则2号囚犯摸到的绿豆数为N+1或N-1.因为2号囚犯可以通过摸剩余绿豆的方法得知1号囚犯摸到的绿豆数,2号囚犯摸到的绿豆数为N的话就会重复是找死,如果摸到的绿豆数与N相差大于1的话,又会使得3号囚犯有机会使摸到的绿豆数居中.

3号囚犯也会使自己摸到的绿豆数与1、2号的紧密相邻,即使自己摸到的绿豆数比1、2号的之中最大的大1,最小的小1.因为3号囚犯可以通过摸剩余绿豆的方法得知1、2号囚犯摸到的绿豆总数,又知1、2号囚犯摸到的绿豆数相差为1,从而判断出1、2号囚犯各自摸到的绿豆数.

4、5号囚犯与3号囚犯想法基本相同.即使自己摸到的绿豆数比自己前面所有的之中最大的大1,最小的小1.

综上所述,5个囚犯摸到的绿豆数为5个连续整数.

1号囚犯存活机率.1号囚犯有两种情况必死：摸到的绿豆数最大或最小.摸到的绿豆数最大或最小,只能由后4位囚犯决定,由分析可知后4位囚犯的摸到绿豆数的位置都只有两个,即一组连续整数的两边.因此1号囚犯摸到的绿豆数为最大时的机率为（1/2）*（1/2）*（1/2）*（1/2）=1/16,最小时的机率也为1/16,1号囚犯存活机率为1-（1/16）*2=7/8

2号囚犯存活机率.由对称性可知2号囚犯存活机率与1号相同,也为7/8.3号囚犯存活机率.3号囚犯摸到的绿豆数为最大时的机率为（1/2）*（1/2）*（1/2）=1/8,最小时的机率也为1/8,1号囚犯存活机率为1-（1/8）*2=3/4.

4号囚犯存活机率.4号囚犯摸到的绿豆数为最大时的机率为（1/2）*（1/2）=1/4,最小时的机率也为1/4,4号囚犯存活机率为1-（1/4）*2=1/2.

5号囚犯存活机率.5号囚犯摸到的绿豆数不是最大就是最小,必死无疑.5号囚犯存活机率为0

4、设开始有x个椰子,我们把x写成(x+4)－4．

第一个人来了,分给猴子1个,此时还有椰子

(x+4)－4－1=(x+4)－5,

这时恰好可分成5份,每份的椰子数为

[(x+4)－5]/5=(x+4)/5－1

(x+4)/5必须为整数,所以（x+4）是5的倍数,

第一个人拿走一份后,剩下的椰子为：

（4/5)×[(x+4)-5]＝(4/5)×(x+4)－4

同样,第二个人来了,分给猴子1个,拿走一份之后,剩下的椰子数为

(4/5)×[(4/5)×(x+4)－5]

由于(4/5)×(4/5)×(x+4)是整数,故（x+4）应是5×5＝25的倍数,

如此一来五个人一分一拿,恰好剩下

(4/5)×(4/5)×(4/5)×(4/5)×(4/5)×(x+4)-5个椰子,

故(x+4)必须是5×5×5×5×5的倍数,

即x+4=5^5

所以：x=3125-4=3121

即开始最少有3121个椰子．有人是这样解的,究竟谁对谁错呢?

3121是错的,因为最后还要分一次

(4/5)×(4/5)×(4/5)×(4/5)×(4/5)×(x+4)-5必须还要被5整除,x+4至少是5的6次方的倍数：5×5×5×5×5×5=15625,总数就是：15625-4=15621个

5、第一箱子拿1块，第二箱子拿2块， 第n箱子拿n块，然后放在一起称，看看缺了几钱，缺了n钱就说明是第n个箱子。

6、第一个瓶可拿出1片，第二个拿2片，第三个拿3片，但第四个不能拿4片，因为如果结果缺了5克的话，你就不知道是缺了2+3还是1+4。所以第四个应拿5片，第五个应拿8片，第n个应拿a(n-1)+a(n-2)片。

以上就是贤知助手为大家整理的有关于如何从逻辑思维题训练打破常规思维的全部内容了。