如何培养“数感”，为什么说是小学数学教育的主要目标？

今天跟大家讨论一下数感这个玄乎的东西，文章很干货，主要分三部分内容，之前对数感有过了解的朋友可以捡自己感兴趣的部分去看：

1.什么是数感，以及数感的重要性；

2.我们很多时候是在破坏数感；

3.培养数感的方法。

咱们目前普遍认为初等数学的教学有两个功利性的目标：

• 为日常生活提供计算工具；
• 为提升思维水平提供智力训练。

  过去，在我上小学的年代，小学数学叫“算术”，以第一个目标为主要目标。

  当时，每年到我家杀猪的时候，就是我大显数学才能的时机，谁家买了几斤多少钱，快速算出并记下。

  现在人人手机里都有计算器，再到这杀猪的场景，估计大家都是按按手机，不会再有人傻到用我小时侯的方法了。

  所以，第一个目标似乎正在变得无意义。

  于是，新的美国学校数学课程与评估标准（NCTM）强调要将培养学生形成数感作为小学数学教育的主要目标。并明确反对在小学数学教育中过分强调没有思维的计算程序。中国的新教纲也与时俱进，将数感提到了非常重要的地位。

  

  那到底什么是数感？它为什么如此受重视？

  有人说数感就是对“数”有感觉，有点玄学的味道有没有？也有人说，数感就是对“数”有洞察力，还是有点玄。

  我觉得本质上，数感好的孩子就是在数与数之间建立了很多联系，因为有了这种联系，在不同的问题中就有了各种“灵活性”和“创造性”。

  举个例子：

  一个数感好的孩子看到98时，不仅会想到它是“90+8”，也是“100-2”，还是49的2倍。

  于是，当计算类似“98+76”时，ta就不需要使用竖式，直接从76中拿2个给98。心算一下就知道是174了。

  当计算类似“98+49+50+52”时，ta也不列竖式，而是有脑中完成以下的计算过程：

  98+49+50+52

  =50 × 5 -2-1+2

  =249

  所以，培养数感，不是在弱化计算能力，相反它是在增强计算能力。

  只是，现在计算不再是单一的模式化，而是要求更多的灵活性和创造性。

  在美国学校数学课程与评估标准中，数感也正是和计算策略中的“灵活性”与“创造性”一起出现的。

  因为强调“灵活性”与“创造性”，所以就要求理解力，以及主动思考的积极态度。这两者同时也正是进入数学殿堂最重要的必备素质。

  而且因为这种“灵活性”与“创造性”，使得学生不停地探索数与数之间的各种关系，这种数与数之间各种关系的熟悉感，不单是对计算能力有很大帮助，几乎对整个数学学习生涯都有莫大的帮助，比如因式分解、数列的收敛等等；但计算能力好，可能就只限于小学阶段考个好分数了。

  所以强调数感的培养，不仅有助于计算能力的提升，还将促进理解力的提升，和养成主动思考的积极态度。

  而过份重视程序化计算能力（如竖式的熟练度）的训练，将很容易惰化思维。我想这也是NCTM中明确反对它的根本原因。

  普遍用计算器的标准来衡量孩子的计算能力

  让我们先来看一个学校二年级学生的计算能力检测标准：

  

  我也不时收到有朋友发来的类似这样的疑问：

  “老师今天发了一张纸，是所有两个数的和等于11的算式，让小朋友今天背会。孩子背起来很困难，为什么会有这样的数学作业？”

  还有喜欢研究新教育方法的家长朋友在推荐印度数学和日本数学，说它们可以让孩子算得又快又准又好玩。

  

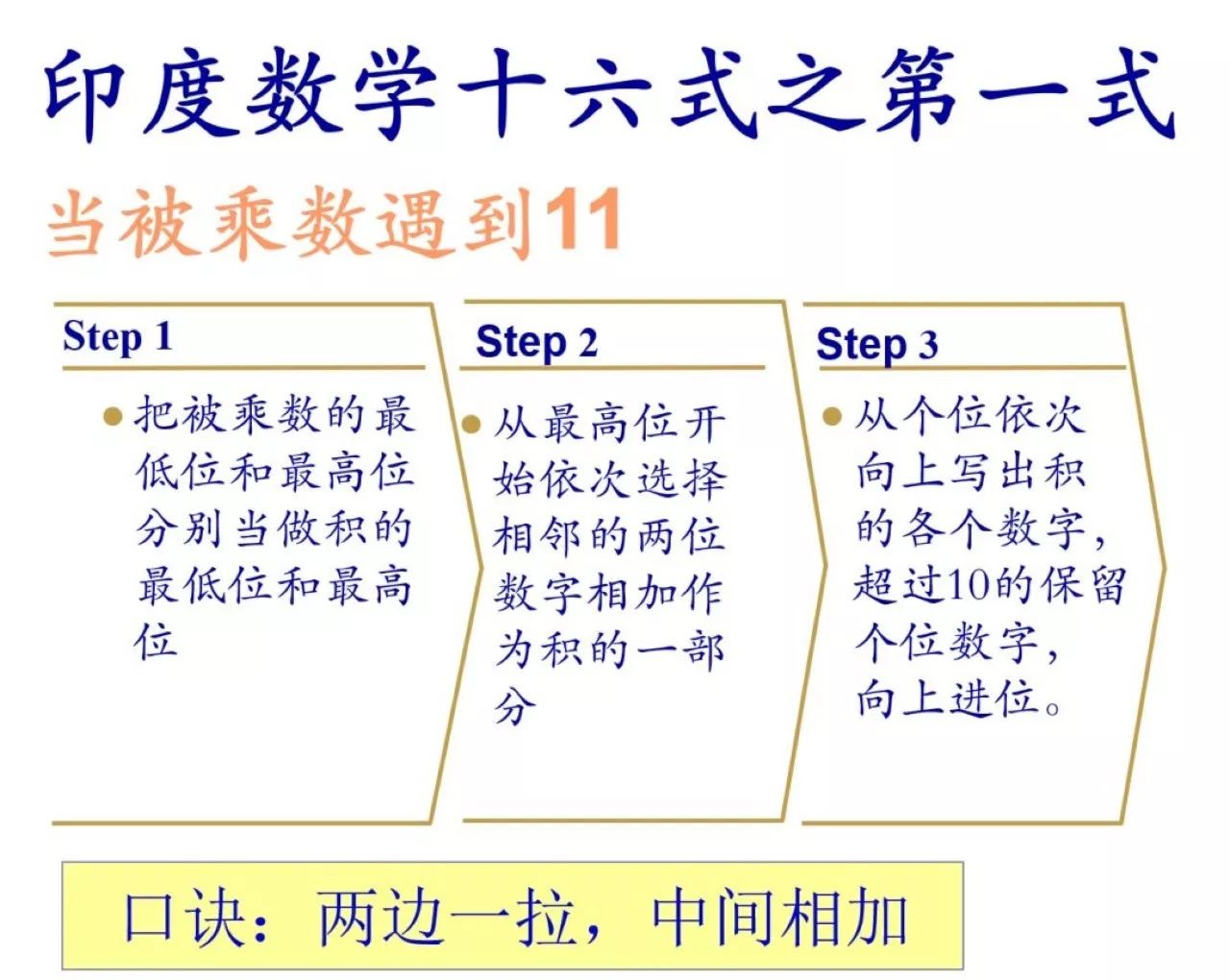
  印度数学十六式

  

  日本数学

  类似的还有许多……

  所有的这一切，都可以看出教育者的功利。只是，有的粗暴些，有的含蓄些。但本质是一样的。

  他们都有试图对孩子的大脑进行编程，植入一套程序，然后让孩子快速准确地解决计算问题。

  可是，这和我们编一个计算器程序有什么不同呢？

  当我们花好几年时间将孩子编成一台偶尔还会出错的计算器时，该喜还是该悲？

  也许，在这些教育者的认知中，数学就是计算，计算就是数学。

  大量程序化的计算是培养数感的天敌

  程序化的计算指的是什么？上面说过的——

  ▪ 印度数学十六式

  ▪ 日本数学计算大法

  ▪ 我们整天练的竖式

  类似的计算方式都在这个范畴里。

  因为这些计算方法有固定的计算步骤，使用者不需要去理解背后的原理，照猫画虎，都能算对。因此这类计算，被普遍认为是没有思维过程的。

  没有思维过程，意味着每次都只是进行着程序上的机械性重复。

  因为是机械性的重复，又意味着每次的练习除了提升这种程序的熟练度之外，没有太多额外的收获。

  更加要命的是，这种长时间持续的机械性重复训练，给很多孩子养成了一种严重的思维惰性。从而失去了学习观察的机会，失去了主动思考的意识。这将遗毒无穷……

  看到过好多6年级孩子，他们很熟练地计算着6666÷2222=3，但在综合算式中，怎么都看不出——6666 是 2222的3倍。

  还有好多孩子在计算类似：1/16+ 1/24 时，他们的计算过程也是完全程序化的：

  1/16+ 1/24

  =16/（16×24）+24/ （16×24）

  =40/384

  =5/48

  对他们来说，一下看出48是16和24的公倍数是很困难的。如果提醒，那他们就一定要使用一遍短除法才能找出它们的公倍数。所以，对他们来说，还不如用前一种方法来得更快。

  出现这种状况的根本原因，就在于日常大量的程序化计算练习，使得他们：

  ▪ 失去了很多观察数与数之间的联系和关系的机会；

  ▪ 失去了很多创造性地进行计算的机会，从而也失去了计算带来的乐趣；

  ▪ 养成了对计算的条件反射式的反应，其实也就是思维上的惰性。

  所以，我说大量程序化的计算是培养数感的天敌，其遗毒无穷。

  更可怕的是，现在这种功利性的程序化计算训练还在往幼儿中渗透。

  前段时间看到一篇文章《幼儿园学生1分钟攻下小学数学》，一个叫Mandy的老师发明了Mandy数学，将20以内的进位加法完全变成了一个抽象的加法表上的程序化动作。

  这些幼儿正是在构建数量、以及加减概念的关键时期，极需在更多具体实际场景中建构数与量之间的对应关系，建构加减法与数数之间的对应关系。这种程序化的抽象训练将极大地影响和破坏这一过程。

  

  那么，提高数感应该从哪些方法着手呢？

  在情境中进行运算

  在情境中进行运算，有很多好处。

  因为运算有了具体场景，而小学阶段孩子们的思维不是完全抽象式，是必需借助于具像的事物或场景。

  有了思维可依托的场景，就可以进行思考。有了思考，就有了各种创造性的可能。孩子越小，数学能力发展越慢的孩子，这就越重要。

  但很多教育者着急，就象前面说的那个Mandy老师，老想着快速越过这个阶段，然后就是大量的程序化的计算练习。这样练习的结果就是，虽然看着孩子们能快速进行某类计算，但他们并不理解背后的原理，也就对其思维水平的提升帮助极少。

  这种欲速则不达的道理，在很多高年级孩子身上都不停地得到印证。

  概念为本、算理为先

  我先讲两个有阶段性计算障碍的例子。

  第一个例子：

  一个3年级的孩子，由于之前出国了一年多，虽然在国外也在上学，但由于语言等原因，数学学的很不系统。

  回国学习一段时间后，在乘法运算等方面都遇到了比较多的困难。学校在教乘法竖式，他学不会。

  其实，学不会的孩子是比较好办的。学不会，说明孩子不愿意接受他不理解的事物。要不然，对没有智力障碍的孩子，那么复杂的电子游戏都无师自通，谁会模仿不了那些简单的套路。

  这说明他们在智力上是自律的，内在心智不随便接受权威，而是根据自己的逻辑结构来判断。

  这种孩子，只要让他真正理解了概念和算理，一切就都OK了。

  于是，我给他重点设计了两类练习。

  一类练习让他理解数位和计数单位的概念。比如任何3位数ABC都可以按需要很自然地看成：A个100+B个10+C，当然也可以看成 ：AB 个10 +C。

  另一类练习，让他在具体场景中去理解去做乘法的练习。

  比如：一箱苹果25个，48箱共几个苹果呢？

  列式是：25 × 48，计算时，我可以先算40箱的个数，再算8箱的个数，再加起来。

  所以，计算就可以变成：

  25 × 48

  =25×40+25×8

  =1000+200

  =1200

  这就是乘法运算过程中最基本的算理，不管是竖式、印度数学还是日本数学，乘法运算背后的算理都是这个。

  小伙子很快就将这个算理掌握和理解得非常好了。我甚至都没他讲解过一次乘法的竖式，也没做过任何竖式的练习。三个这类的练习之后，他对乘法竖式一下就理解了。之后计算能力一直保持得很强，也很少出错。

  第二个例子：

  这个是四年级的孩子，在3年级结束后的暑假接触到他的数学。他当时对除法运算，对多位数除以一位数的除法运算完全是混乱的。

  同样道理，对没有智力障碍的孩子，他学不会他应该能学会的内容。说明他在智力上是自律的，是在内心不愿接受他不理解的事物，所以不愿意去接受套路。

  我只花了半个多小时的时间和他一起研究了除法竖式的算理。他又练习了半个多小时，然后除法运算对他就是小菜一碟了。

  后面他再学多位数除以多位数的除法，小数的除法，也没再遇到任何障碍。

  所以，在学运算时，概念是根本，只有概念清楚，才能做对心中数，对一切变化都了然于胸。算理清楚了，才能生发出各种各样的创造性和多变性。使计算过程更简单、更有趣。

  

  推迟标准化计算程序的训练

  像前面提到的竖式、印象数学十六式、日本数学等，都属于标准化计算程序的一种。这些方法的主要特征，就是人们在使用这种方法进行运算时，甚少进行思维活动。

  为什么要推迟进行这种标准化计算程序的训练呢？

  一个是因为这种长期、机械的简单重复训练，让人极易产生思维惰性。这种思维惰性一经产生，它就是一种惯性，要改变就会很困难。

  思维惰性和创造性、灵活性是天生的敌人，而数感正是从创造性和灵活性中得来的。

  另一个是因为一旦标准化计算程序得到很熟练的掌握后，孩子就没有积极探索各种计算策略和方法的动力了。

  比如在计算：99 × 98 时，竖式乘法很熟练的孩子，不会再有任何想法。

  没学竖式的孩子，就会从概念和算理角度来考虑：

  99 × 98 可以看成是99个98相加，它和100个98减去1个98是一样的

  于是：

  99 × 98

  =100× 98-98

  =9800-98

  =9702

  在学各种标准化的计算程序（如竖式）之前，让孩子们有充分的时间和机会去探讨和研究计算的多样性和灵活性。非常有助于孩子们真正理解算理，对数感的培养会有非常大的促进作用。

  多听少教

  除了书面的练习，孩子们非常需要在以孩子的思维活动为主的对话中进行学习。

  这种对话式的学习环境会促进他们主动地寻找独立解决问题的方法。而教育者在对话过程中通过问题启发孩子进一步的深入思考。有了思维活动，孩子就有了学习如何观察、实践着各种灵活多样的创造性的机会。还可以有机会比较自己和他人所使用的不同的策略。

  这个过程中，孩子不仅可以体会到自己的思考和创造得到别人认可所带来的快乐，还能不断地同化和顺应着自己接触或创造的不同概念和方法，从而促进其思维水平不断向前发展。

  但这种的对话过程中，也存在一些常见的误区：

  1、容易把对话过程变成一种纠错过程，我们往往会抓住孩子的一两个小错误不放。这将极大地大击孩子的积极性和思维的兴奋度。所以我们应该多听、多问、少教。让孩子能够顺畅地按照自己的思路来组织语言。

  2、容易把对话过程变成一处教学过程。教育者，特别是家长，在进行这种对话时，很容易就想把自己知道的相关知识和方法教给孩子，对孩子笨拙的描述和方法通常不能保持耐心。

  但我们要知道，教育的目的不是为了解当前这个问题，而是要促进孩子思维水平的发展。而思维水平的发展，是依赖于他们自己的积累。

  所以，任何自主的思维过程都是有价值的，都应该鼓励其继续下去。

  鼓励心算

  通过之前的讨论，我们已经知道，孩子们数感强弱的根本就在于数与数之间的联系多少。

  而心算恰恰就会要求孩子去考虑计算策略的选择，计算策略的选择过程又会要求孩子不断地对数进行重组，最终刺激孩子不停地思索数与数之间的关系。

  这种心算的练习，将会极大地加强数与数之间的联系，对孩子的数感培养起来很大的促进作用。同时，心算对运算规则的理解也有极大的帮助。

  PS：这里的心算不是指珠心算，珠心算是图像式的记忆运算，对数感的培养正面作用甚少。