初一数学知识清单：数轴、相反数与绝对值

二、数轴、相反数与绝对值

　　1．数轴的定义与画法

　　（1）数轴的定义：

　　规定了原点，单位长度和正方向的直线叫数轴，任何一个有理数都可以用数轴上的点表示．

　　注意：数轴上的点不都表示有理数．

　　（2）数轴三要素：原点，单位长度，正方向．

　　（3）数轴的画法：

　　①画一条水平的直线；

　　②选择合适的位置作为原点；

　　③选择向右的方向为正方向，用箭头表示；

　　④选择合适的长度作为单位长度，向右标正、向左标负．

　　2．相反数

　　（1）相反数的定义：

　　如果两个数只有符号不同，则我们称其中一个数为另一个数的相反数，也称这两个数互为相反数；特别地，0的相反数是0．

　　（2）相反数的性质与判定：

　　①相反数的性质：互为相反数的两个数相加得0；

　　②相反数的判定：如果两个数的和为0，则这两个数互为相反数．

　　（3）相反数的几何意义：

　　在数轴上，表示互为相反数（零除外）的两个点，位于原点的两侧，并且到原点的距离相等．

　　3．绝对值

　　（1）绝对值的几何意义：

　　把一个数在数轴上的对应的点到原点的距离叫做这个数的绝对值，一个数a的绝对值表示为 ；

　　（2）绝对值的代数意义：

　　一个正数的绝对值是它本身；一个负数的绝对值是它的相反数，零的绝对值是零，互为相反数的两个数的绝对值相等．

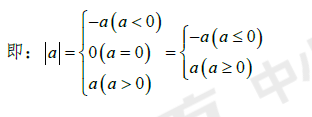
　　（3）绝对值的非负性：

　　任何数的绝对值都不是负数，即 （ 为任何数）．