初一数学知识点——有理数大小比较

　　初一数学，在初中三年的课程里其实是最简单的，因为到了后期，很多知识点都是叠加的，所以，大家要在初一的时候打好基础。

　初一数学知识点——有理数大小比较

　　（1）有理数的大小比较

　　比较有理数的大小可以利用数轴，他们从左到有的顺序，即从大到小的顺序（在数轴上表示的两个有理数，右边的数总比左边的数大）；也可以利用数的性质比较异号两数及0的大小，利用绝对值比较两个负数的大小．

　　（2）有理数大小比较的法则：

　　①正数都大于0；

　　②负数都小于0；

　　③正数大于一切负数；

　　④两个负数，绝对值大的其值反而小．

　　【规律方法】有理数大小比较的三种方法

　　1.法则比较：正数都大于0，负数都小于0，正数大于一切负数．两个负数比较大小，绝对值大的反而小．

　　2.数轴比较：在数轴上右边的点表示的数大于左边的点表示的数．

　　3.作差比较：

　　若a﹣b＞0，则a＞b；

　　若a﹣b＜0，则a＜b；

　　若a﹣b=0，则a=b。

初一数学有理数比大小练习题

1、利用数轴比较大小

　　可以利用数轴比较大小，数轴上，越往右越大，越往左越小。有些题目需要结合绝对值和相反数的概念，互为相反数的两个数在原点的两侧，到原点的距离相等。

　　例题1：已知a＞0，b＜0，且|a|＜|b|，试比较a、-a、b、-b的大小．

　　分析：由于a＞0，b＜0，则a在原点的右边，b在原点的左边，又|a|＜|b|，知a离原点的距离小于b离原点的距离，在数轴上表示出a，b，再根据一对相反数在数轴上的位置特点：分别在原点的左右两边，并且离开原点的距离相等，在数轴上又可以表示出-a，-b，最后根据在数轴上表示的数，它们从左往右的顺序，就是它们由小到大的顺序，从而得出结果．

2、特殊值法比较大小

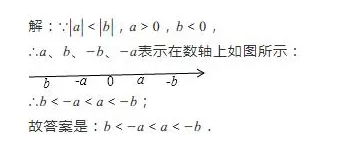
　　有些小题无法直接比较大小，可以利用特殊值比较大小。比如例题1，可以假设a=2，b=-1，那么-a=-a，-b=1，由于-2＜-1＜0＜1＜2，那么-a＜b＜0＜-b＜a。

　　例题2：已知a＞1，b＞1，且a＞b，试比较a+1/a与b+1/b的大小．

　　分析：由题意可设a=3，b=2，那么a+1/a=10/3，b+1/b=5/2，那么a+1/a＞b+1/b。