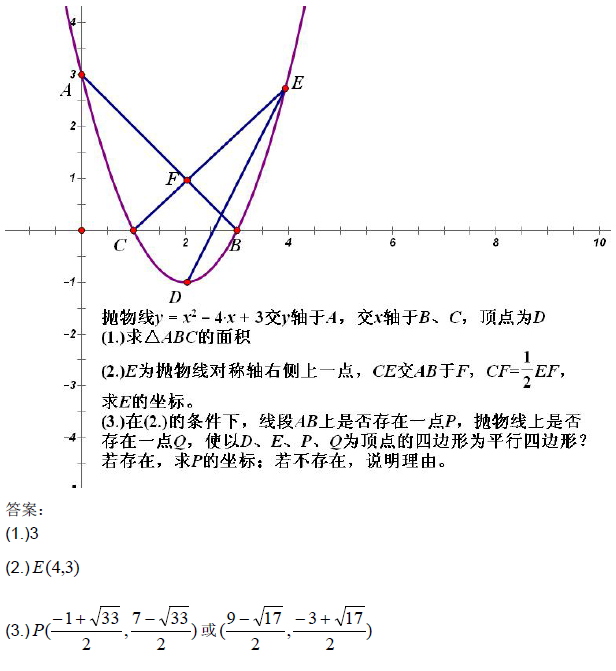
中学数学纠错笔记 —— 四边形存在性问题 —— 平行四边形

　　实用度：★★★★

　　四边形存在性近年来经常考，所以这部分要重视，只是平行四边形考得多了，题型会有创新，

　　因此先打好常规题的基础：一般平行四边形最普通的出题方式如下：

　　普通法

　　函数给出，抛物线交直线于 A、B，在抛物线和直线上分别找 E、F，使得 C、D、F、E 为

　　顶点的四边形是平行四边形。

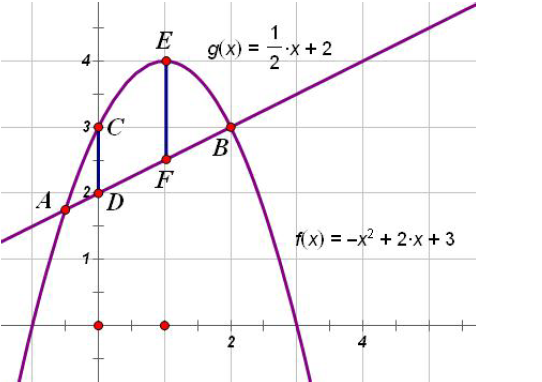
　　这种题十分简单，用上次讲的铅直高表达 EF 和 CD 一等起来就是【以 EF、CD 为对边的平

　　行四边形】注意还没有完，还要讨论对角线的情况，这要取 CD 中点，设坐标转化，然后代

　　入函数求解。

　　然后稍微复杂的：作高法

　　这个讲起来就复杂点了，如图

　　函数有，B 的坐标看网格，在抛物线、x 轴上找 P、Q，使以 A、B、P、Q 四点为顶点的四

　　边形是平行四边形，求 P、Q 的坐标

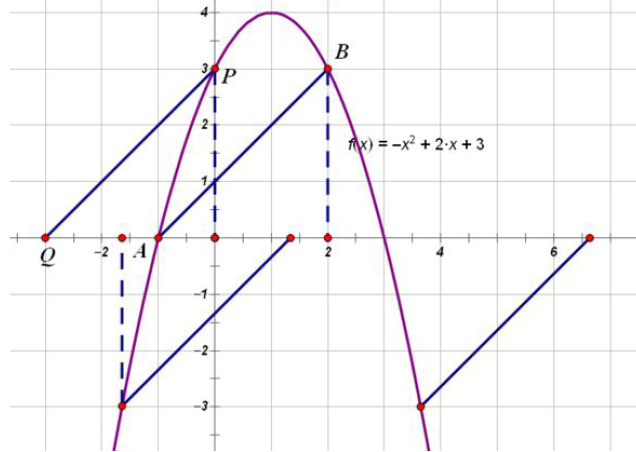
　　先讨论 AB 是边的

　　情况，既然是平行四边形那就先作 PQ‖AB，我们知道，当 PQ=AB 时就是平行四边形。什

　　么时候相等？P 到 x 轴距离和 B 到 x 轴的距离相等，如图，作 PM⊥x 轴，BN⊥x 轴，（图

　　上没画）PM=BN=3 时，就会有△PQM≌△BAN，这样 PQ=AB，就 OK。也就是说，P 的

　　纵坐标是±3 时，因为抛物线有了，解方程即可得到 P 的坐标，因为全等，AN=QM，所以 Q

　　的坐标也有了（？？，0）。另外就是对角线的情况，同样找中点转换。

　　变式：

　　万一题目条件不变，Q 改成在对称轴或者某常函数上找要怎么办？

　　事实上是一样的：只是歪了点而已，记住两边都有，别只找到一边不找另一边。

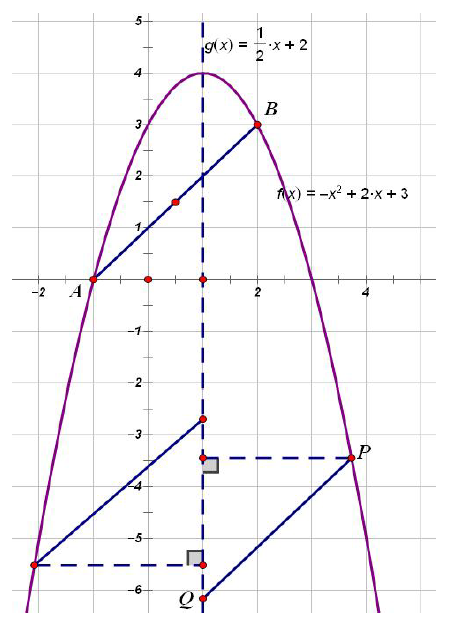
　　【例题】（原创）难度：★★★